Python(素数イテレータ)

フィボナッチ数と同様に特殊メソッドを用いて素数を返すイテレータを作成しました。また今回は時間を計測するデコレータを自作し、処理時間についても考えていきたいと思います。

class Prime:
    def __init__(self,x=10,*,mode=0):
        """@param x     閾値(default=10)
           @param mode　0＝個数　1＝最大値（default=0）"""
        if not Prime.is_num(x) or not Prime.is_num(mode)\
           or (mode < 0 or mode > 1):
            raise ValueError
        
        self._x = x
        self._mode = mode

    @staticmethod
    def is_num(x):
        return isinstance(x,int)

    @property
    def mode(self):
        return self._mode

    @property
    def threshold(self):
        return self._x

    @mode.setter
    def mode(self,value):
        if not Prime.is_num(value) or (value < 0 or value > 1):
            raise ValueError
        self._mode = value

    @threshold.setter
    def threshold(self,value):
        if not Prime.is_num(value):
            raise ValueError
        self._x = value
        
    def __str__(self):
        return "prime numbers"
    
    def __iter__(self):
        self._count = 0
        self._num = 1
        return self
    
    def __next__(self):
        if self._mode == 0 and self._count >= self._x:
            raise StopIteration
        
        is_prime = False
        self._num += 1
        while not is_prime:            
            is_prime = True
            for i in range(2,self._num):
                if self._num % i == 0:
                    is_prime = False
                    break
            if is_prime:
                break
            self._num += 1

            if self._mode == 1 and self._num >= self._x:
                raise StopIteration
        self._count += 1
        return self._num

# デコレータ関数の定義
def show_func_name(func):
    def wrapper(*args,**kwargs):
        print("---start:" + func.__name__)
        res = func(*args,**kwargs)
        print("\n---end:" + func.__name__)
        return res
    return wrapper

# 処理時間を計測するデコレータ関数の定義
def time_log(func):
    def wrapper(*args,**kwargs):
        import datetime
        start = datetime.datetime.today()
        print("---start:" + func.__name__)
        res = func(*args,**kwargs)
        end = datetime.datetime.today()
        delta = end - start
        print("\n---end:" + func.__name__,delta,"sec")
        return res
    return wrapper

p = Prime()
print("str:",str(p))
print("mode:",p.mode,"threshold:",p.threshold)

@time_log
def test_iter():
    for i in p:
        print(i,end=" ")

test_iter()

p.mode = 1
p.threshold = 200
print("\nmode:",p.mode,"threshold:",p.threshold)
test_iter()

Primeクラスの仕様については Python(フィボナッチ数イテレータ) のFibonacciクラスと同様でmodeを指定することで閾値を変える事ができるようにしています。

素数の抽出はフラグ管理で自身の数までに約数があれば素数ではないと判別し、約数がなければ素数なので、その数を返すようにしています。
この処理ではforループで毎回カウントアップしながら約数があるかどうかのチェックをしているため、数が多くなるほど時間がかかってしまいます。

実際に10000までの素数をイテレータで計測した場合の時間が以下のようになりましたが、printをするかしないかでも大きな時間差が･･･
どうやらIDLEでディスプレイ表示させるのには、かなりのコストがかかっているようでした。

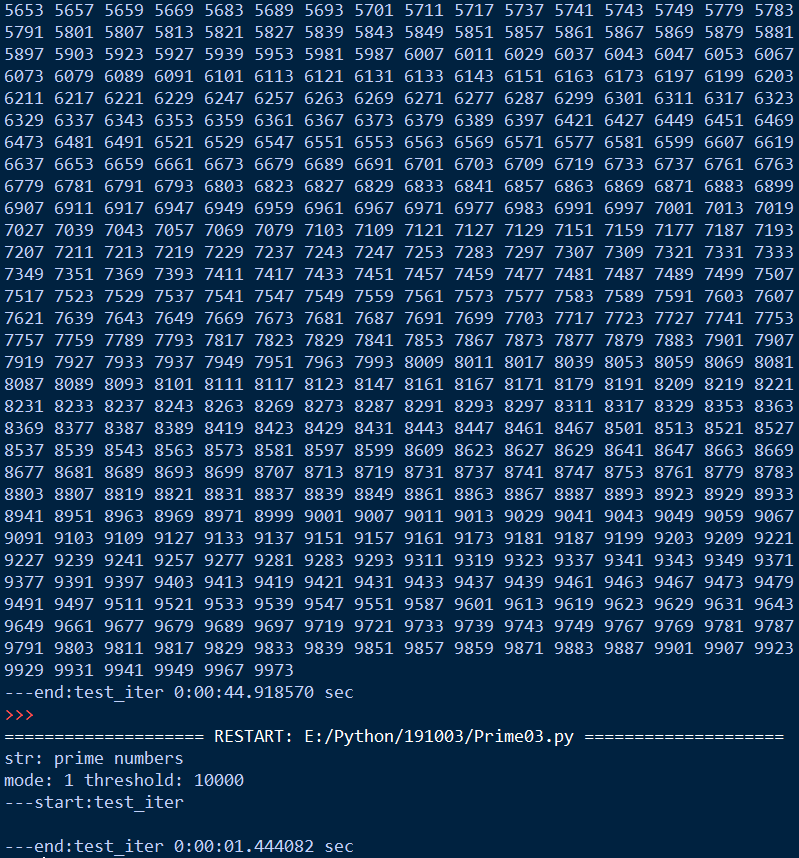
素数抽出アルゴリズムでは「エラトステネスのふるい」という効率的なものがあるので、それをふまえた抽出プログラミングにもチャレンジしたいと思います。

今回はデコレータを自作しているので、デコレータって何？という部分を次回投稿で記載したいと思います。